Leaves and creases Pt2

I’ve written before on Leaves and creases (and I’ve just improved the post a bit), but today, on a hot day, I’m thinking about banana leaves and folding.

My previous post discussed different surfaces created by the ribs and how they are used for stiffness. This lovely paper showed that typical hierarchical leaf vein patterns are all about nutrient transport, not structural stiffness. The money shot is the two figures reproduced below. It’s really clear that most leaves are optimised for nutrient transport.

Optimised leaf vein patterns for nutrient transport in different creased surfaces

Optimised leaf vein patterns for stiffness in different creased surfaces

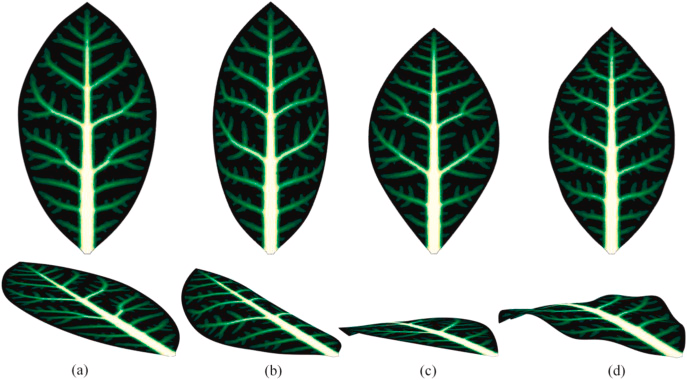
So. Why are banana leaves different?

Banana leaves are interesting because they are quite large, and quite simple. They have a single ‘spine’ stem that runs along the leaf, and the veins then all run off that spine at right angles. In this metaphor, they are closer in nature to ribs then the spreading pattern of veins in most leaves. They are of interest, as simple hierarchies and right angles are much easier to build. Why does the banana have this pattern?

In the previous post, I talked about Crocosmia, and how it is an interesting cantiliver, but also how it folds it’s leaves up when it is too dry. Banana plants do this too (pic below). This may be to reduce solar gain, it may be in anticipation of heavy tropical rain that could damage the leaves.

Drooping banana, with a background of drooping grass, drooping crocosmia and indifferent bramble (too stiff and spiky to droop).

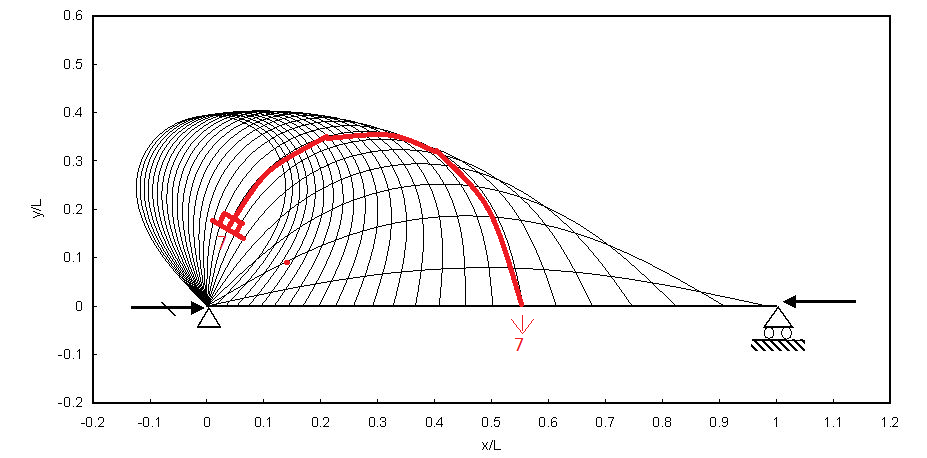
There’s some interesting things going on here. The central stem is drooping, with the half closest to the trunk following a normal cantilever beam deflection curve (approximately a constant radius). The end of leaf is drooping so much that gravity is practically straightening the spine out again, and between there’s a transition between those extremes. The fixed radius approximation is really only close to true for very small deflections, which is one reason structural engineering design codes limit deflection to very small amounts. It does make the maths a lot easier, not that nature cares much about that.

What we actually have (I think) is a portion of an elastica curve, image below. (link to image source and inspirational blog) (PDF link to a math paper). Why an elastica curve? Zero moment at the tip/pin joint, large deformations, a peak moment that is NOT at the fixed point of the cantilever, and a constantly transitioning curvature.

Ok, so the stem is dropping following some continuous curve. Why are the leaves folding up? Here, once again, we brush up against developable surfaces. If the starting leaf is a flat surface that doesn’t stretch or squish in-plane (just like a sheet of paper), then it can only take curvature in one direction at a time. It can roll into a cone or cylinder, but not a sphere or a saddle shape. If the stem is drooping in a continuous curve, the surface of the leaf is locked flat with rulings in the other direction and can’t reduce the surface area exposed to the sun. That’s not what we see in the picture, what else is going on?

The same loss of water pressure in the stem that allows it to droop, allows the stem wall to buckle inwards slightly. It allows the rigid ribs to rotate downwards as though hinged (folding inwards, if viewed from above). Since the outside edge of the leaf is just as long as the stem (because they’re normally flat and parallel), all that extra length needs to go somewhere, and depending on your background, you get a ruled surface defined by orgiami pleating, dissimilar sinusoids, or the shape of a buckled flange with constant wavelength. All the same thing.

Simple Origami pleating. Lines marked R are not creases

If we take a simple origami triangle pleating, it doesn’t look quite right. The ribs are all straight, but the folding requires diagonal creases between them and very sharp leaf edges. Lets try a closer rib spacing, and a hit and miss diagonal crease spacing to give us a flat top and bottom to the curves:

Smoother Origami pleating. U marks Up points on the sine wave, D marks down points.

That’s much closer. The diagonal creases are smoothed out in the real leaf, but they need to fit between the tightly spaced stiffer ribs, and spacing of the ribs controls the curvature of the drooping leaf. The final part of the puzzle is that the pleated sections still have self weight, don’t rise above the stem, and since the end of the stem is dropping to a nearly vertical position, it induces a torque that causes the pleats to lay neatly on each other and makes the stem project horizontally slightly more than it would otherwise. This ‘natural’ folding is of interest for movable facades, canopies and flexible solar panels.

In summmary

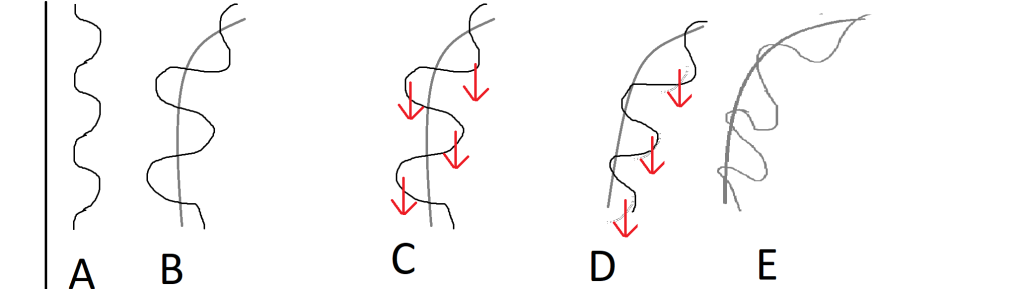
A and B show that the length of the leaf edge and stem are the same, but as the stem droops and the leaf folds the edge needs to fit into a shorter length, so it buckles or pleats, with frequency and curvature controlled by the rib spacing

C the pleats have self weight. If the pleats were equal either side of a vertical stem then it would be balanced and stable. But the stem is not vertical at the trunk end, and only slowly transitions into a vertical droop, if at all.

D Since the pleats MUST hang below the horizontal portion of the stem, (or the fraction of the stem that is travelling horizontally) the pleats all hang below the stem and induce a torque

E The pleats therefore drop further down, overlapping each other, while putting an equal and opposite torque into the stem, causing it to stick out slightly more than otherwise. The stresses are spread evenly along the stem, maximising the material efficiency. As the stem refills with water and stiffens to a more vertical elastica curve, these folds neatly unfold and the banana leaf is restored to it’s nearly flat state.

It’s a lovely theory, but how should it be proved?